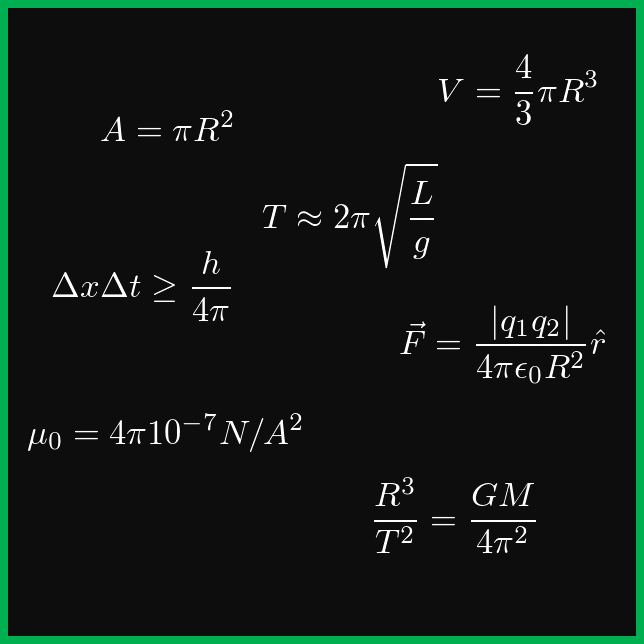
O cálculo de área é um dos primeiros assuntos de matemática ensinados no ensino fundamental. Sempre envolvendo o cálculo de áreas de polígonos regulares como: triângulos,quadrados, trapézios, pentágonos, hexágonos, entre outros polígonos regulares. Todo os polígonos regulares possuem fórmulas matemática intuitivas para o cálculo de suas área como por exemplo os representados pela figura a seguir:

As áreas dos triângulo e dos quadrados são intuitivamente aprendidas, todos demais polígonos regulares podem ser decompostos em uma composição de quadrados e triângulos tornando o cálculo de sua área muito simples. Mas e a área de um círculo? Como sua a fórmula foi descoberta? Qual o parâmetro a ser medido?

Por volta de 400 a.C. um grego chamado Antifome tentou medir a área do círculo enchendo ele de triângulos como mostra a figura abaixo.

No entanto, por mais que esse processo continue, nunca será possível ocupar todo o círculo com triângulos, como mostra a figura abaixo após 3 interações.

Felizmente, nós já sabemos que a área do circulo é igual a , onde R é o raio da circunferência. Porém isto, nos leva a uma pergunta mais interessante: como encontrar o valor de ?

Coube a um grego mais uma vez uma das primeiras experiências que resultou em uma medida aproximada de . O famoso Arquimedes dedicou-se a encontrar uma relação entre o comprimento S da circunferência e o seu diâmetro D. Desta forma, ele encontrou a relação , como o diâmetro é igual a duas vezes o raio podemos escrever, . Além da relação entre o diâmetro e o comprimento o número aparece em muitos outros lugares veja por exemplo estes casos.

Porém, esta forma de medir o valor de é limitada à precisão do nosso instrumento de medida que na melhor das hipótese terá uma precisão da ordem dos milímetros, sem falar que não temos como ter certeza que estão fazendo a experiência em um círculo perfeito.

Então existe alguma maneira de encontrar o valor de exatamente? Com que precisão?

Para medir o valor de , o alemão Ludolf van Cleulen fez um cálculo durante 20 anos usando figuras de mais de 32 bilhões de lados.

Existe alguma maneira de calcular o valor de extamente? Não. Como é um número irracional ele não pode ser obtido com infinitas casas de precisão. No entanto, é possível obtê-lo com a precisão desejada. Uma das maneiras de conseguir isto é usando a série de Gregory-Leibniz.

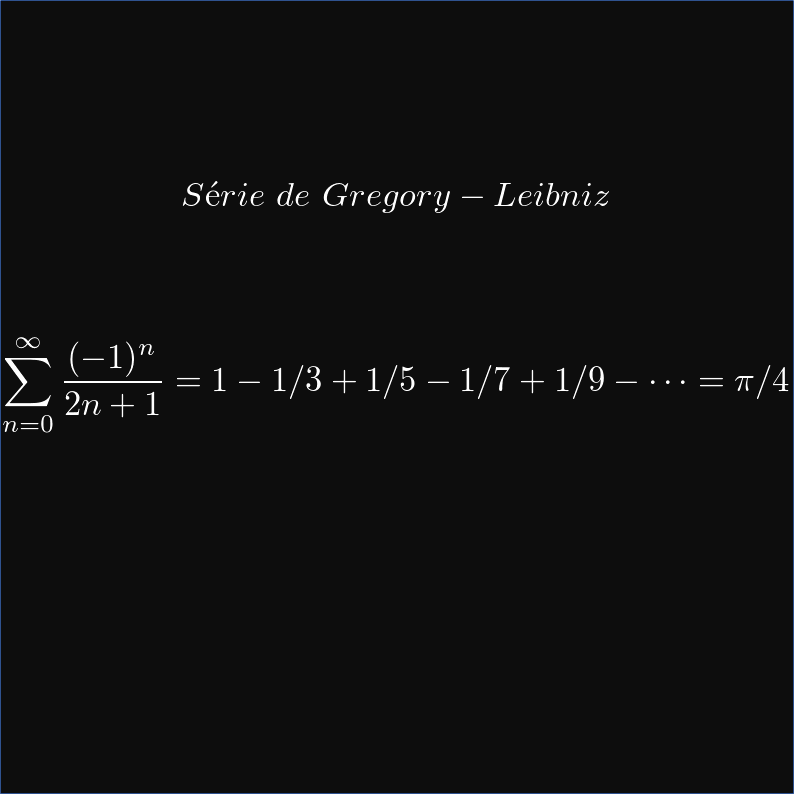
Você só irá necessitar de muita paciência para executar essa conta até atingir a precisão desejada. Abaixo, o valor conhecido para $\latex \pi$ com 100 casas decimais.

Livros recomendados:

• The Historical Development of the Calculus
• Isaac Newton e sua maçã