Aqui farei uma breve explanação breve sobre uma das técnicas que ajudam a visualizar funções complexas, técnica conhecida pelo nome domain coloring.
Em uma função complexa de variáveis complexas, a quantidade de dimensões necessária para a visualização excede as três dimensões usuais. De fato o domínio complexo
pode ser escrito em termos de duas variáveis reais
como
. Ou seja, para visualizar o domínio de uma função complexas precisamos de duas dimensões. A própria função complexa precisa de duas dimensões para ser plotada ( uma para a parte real e outra para a parte complexa). Portanto, precisamos de quatro dimensões para visualizar uma função complexa de uma variável também complexa. Por exemplo, considere
, neste link estão as curvas para as partes real ( em verde) e imaginário ( em vermelho). Compare com a figura 2 deste texto.
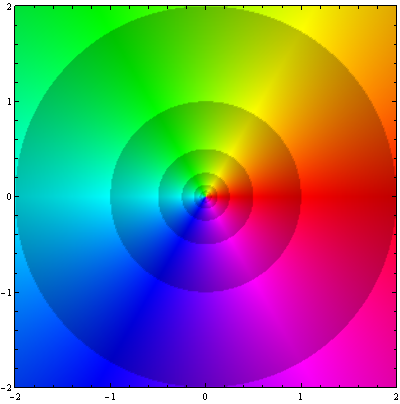
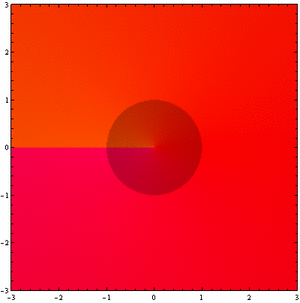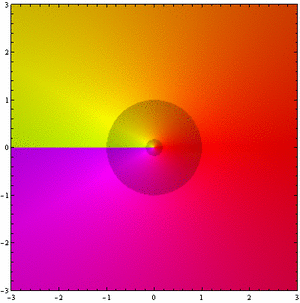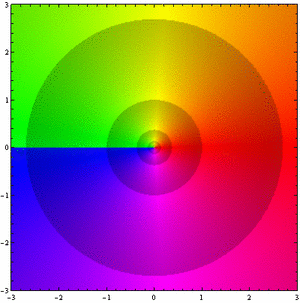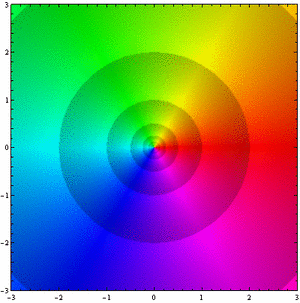
Uma das maneiras de visualizar as funções complexas é usar cores e sombras como dimensões extras. Por exemplo, na figura 1 a técnica de domaing coloring é aplicada à função usando o programa Wolfram Mathematica ( código em no final deste texto). O eixo horizontal é a parte real do domínio e o eixo vertical a parte imaginária. Observe que girando em torno da origem no sentido anti-horário , as cores mudam do vermelho no eixo real positivo, para o verde no eixo imaginário positivo, ao azul no eixo real negativo, ao roxo no eixo imaginário negativo e finalmente, ao vermelho novamente ao completar o ciclo.
As cores representam o argumento da função. Como no exemplo da figura anterior, podemos escrever onde o argumento
tem periodicidade
.
Além das cores, usamos o sombreamento para representar o modulo da função. Note que em ,
e
o sombreamento apresenta descontinuidades. A medida que aumentamos o módulo de
o sombreamento vai se tornando mais escuro até que de maneira descontinua o sombreamento desaparece e o processo se repete sempre que o valor absoluto dobra.
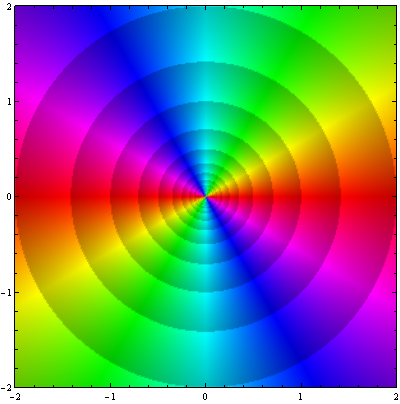
A figura 2, a função . Veja que agora as cores do arco-íris circulam duas vezes ao redor da origem. Podemos compreender isto escrevendo
assim,
. Portanto, o argumento tem periodicidade
. Note que os ciclos de sombreamento tornam-se mais curtos.
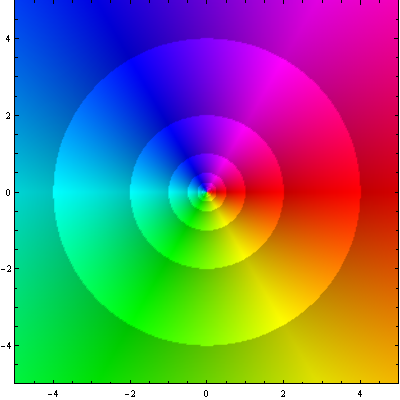
A figura 3 mostra a função . Ao contrário do que ocorria na figura 1, as cores do arco-íris circulam a origem no sentido horário. De fato, os argumentos das duas figuras são o negativo uma da outra. Observe que o sombreamento também acontece em sentido oposto.
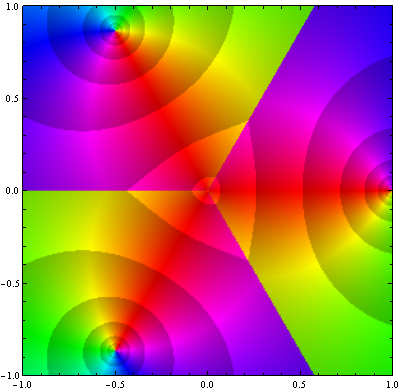
Com estas informações, somos capazes de identifica algumas característica de uma função arbitrária como, por exemplo, a presença de zeros ou de pólos. Além de zeros e polos vamos ver nas figuras a seguir o caso de uma singularidade essencial ( um pólo de ordem infinita).
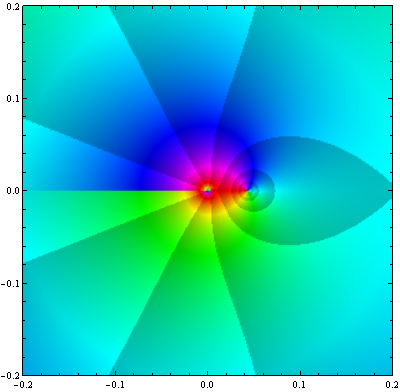
![Exp[z^(-1)]](https://professor-eric.com/wp-content/uploads/2018/02/expz-1.png)
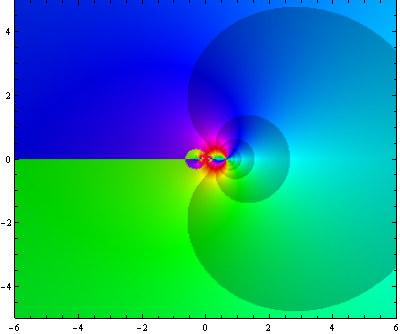
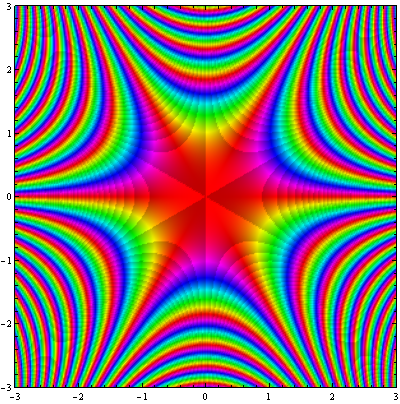
![Exp[z^(-1)] nova escala](https://professor-eric.com/wp-content/uploads/2018/02/expz-1-nova-escala.png)
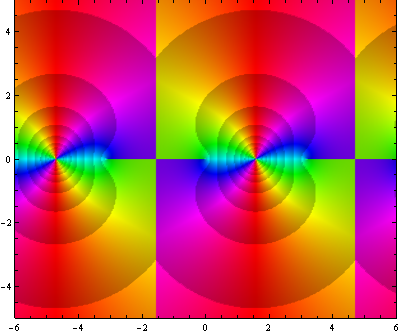
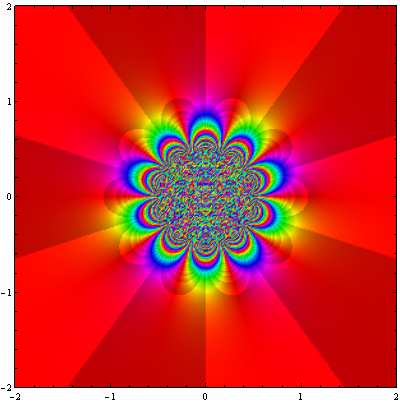
![Exp[z^(-1)] nova escala 2](https://professor-eric.com/wp-content/uploads/2018/02/expz-1-nova-escala-2.png)
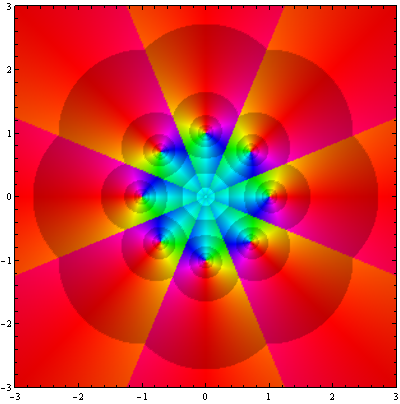
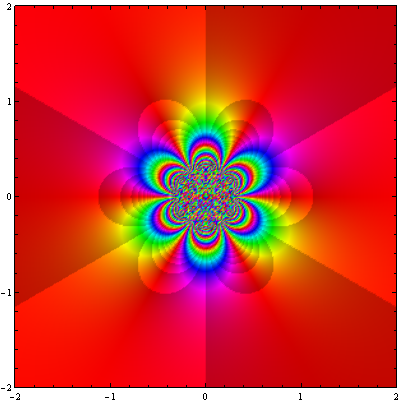
![Exp[z^(-1)] nova escala 3](https://professor-eric.com/wp-content/uploads/2018/02/expz-1-nova-escala-3.png)
As figuras acima representam a função sobre diferente escalas. Na última o programa começa a gerar padrões aleatórios próximo a origem devido a erros numéricos. A razão por traz disto esta relacionada com o grande teorema de Picard, o qual indica que uma função analítica próximade uma singularidade essencial possui todos os valores complexos possíveis, com no máximo uma exceção ( no caso da função
a exceção seria o zero). O ciclo de repetições das cores vai se tornando mais frequente a medida que se aproxima da origem.
Abaixo esta o código do programa feito em Mathematica. E logo em seguida, exibo alguns casos específicos.
PROGRAM
Mathematica code used to generate domain coloring gures:
f[z_] := z;
paint[z_] := Module[{x = Re[z], y = Im[z]}, color =
Hue[Rescale[ArcTan[-x, -y], {-Pi, Pi}]]; shade = Mod[Log[2,
Abs[x + I y]], 1]; Darker[color, shade/4]];
ParametricPlot[ {x, y}, {x, -1.0, 1.0}, {y, -1.0, 1.0}, FrameLabel -> {“x”, “y”},
LabelStyle -> Directive[Black, FontSize -> 22, FontFamily -> “Helvetica”],
ColorFunctionScaling -> False, ColorFunction -> Function[{x, y},
MaxRecursion -> 1, PlotPoints -> 400, PlotRangePadding -> 0,
Axes -> False, paint[f[x + y I]]], Frame -> True,
Mesh -> False, ImageSize -> 500]
![sin[z]](https://professor-eric.com/wp-content/uploads/2018/02/sinz.png)
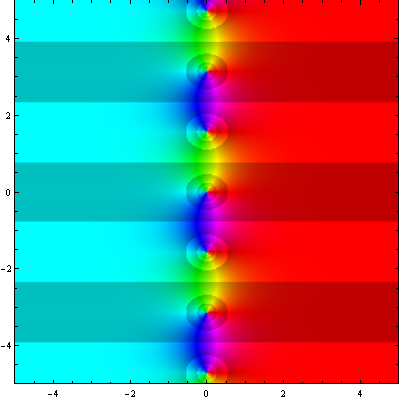
![Tan[z]](https://professor-eric.com/wp-content/uploads/2018/02/tanz.png)
![Exp[z]](https://professor-eric.com/wp-content/uploads/2018/02/expz.png)
![Exp[-z^2] nova escala](https://professor-eric.com/wp-content/uploads/2018/02/exp-z2-nova-escala.png)
![ArcTanh[z^(-5)]](https://professor-eric.com/wp-content/uploads/2018/02/arctanhz-5.png)
![ArcTan[z]](https://professor-eric.com/wp-content/uploads/2018/02/arctanz.png)
![ArcTanh[z^(-1)]](https://professor-eric.com/wp-content/uploads/2018/02/arctanhz-1.png)
![1 por Cos[z]](https://professor-eric.com/wp-content/uploads/2018/02/1-por-cosz.png)
Mais algumas funções escolhidas aleatoriamente.
Para mais informações consulte estas fontes: https://gandhiviswanathan.wordpress.com/2014/10/07/domain-coloring-for-visualizing-complex-functions/
Data Visualization: a successful design process (English Edition)
Data Visualisation with R: 111 Examples
http://www.mi.fu-berlin.de/en/math/groups/ag-geom/news/Domain_coloring.html .






Deixe um comentário