Estimulado pela postagem do Washington Post, eu resolvi fazer minha própria versão da simulação da propagação de uma epidemia em um ambiente fechado. Você pode baixar a minha versão feita em python por meio deste link (sinta-se livre para baixar e alterar o programa a vontade mas peço que me cite como autor). Quero deixar bem claro que meu único objetivo é analisar o caráter estatístico do processo, não levando em consideração aspectos sociais que podem estar envolvidos.

O modelo consiste de simular o contato entre pessoas substituindo-as por bolinhas que vagam livremente como as moléculas de um gás ideal. Diferentemente da simulação do Washington Post, eu não fiz com que as bolinhas colidissem umas com as outras. Essas colisões contribuem para limitar a difusão de partículas e distância a simulação da realidade uma vez que as pessoas não necessariamente mudam seu trajeto simplesmente por terem encontrado alguém na rua. As bolinhas vermelhas representam as pessoas saudáveis e as bolinhas azuis representam as pessoas doentes. Para não ser mal interpretado e não gerar confusão com alguns termos técnico da área da medicina, eu resolvi escrever um pequeno “glossário” próprio para este texto (dito de outra forma, a definições abaixo não são as definições formais aceitas pela comunidade cientificá, porém isso não prejudica em nada o raciocínio do problema).

• doente: pessoa capaz de transmitir a doença independentemente de apresentar ou não sintomas.
• Saudável: pessoa incapaz de transmitir a doença
• Tempo de transmissão: Tempo em que uma pessoa doente (bolinha azul) pode transmitir o vírus se entrar em contato com uma pessoa não imune.
• Imune: Pessoa que é incapaz de ser infectada (para a simulação, após o tempo de transmissão a bolinha se torna vermelha novamente e é incapaz de infectar outras pessoas e, também, de ser infectada novamente.)
• Tempo total de epidemia: o tempo para que a última pessoas contaminada perca a capacidade de transmitir o vírus a outros.
• Pessoas não infectadas: pessoas que durante todo o tempo total de epidemia nunca tiveram contato com a doença.

Na simulação, por enquanto, não há a possibilidade de morte ou de reincidência. A seguir estão alguns vídeos da simulação. Para cada vídeo eu vario o número de pessoas dentro desse quadrado que limita as bolinhas. O gráfico abaixo representa no eixo y o número de pessoas “doentes” pelo tempo no eixo x.

Daqui pra frente irei mostrar apenas os gráficos e deixar as simulações de lado.

Variando o número de pessoas com o tempo de transmissão e a área total fixos

Tempo total de epidemia

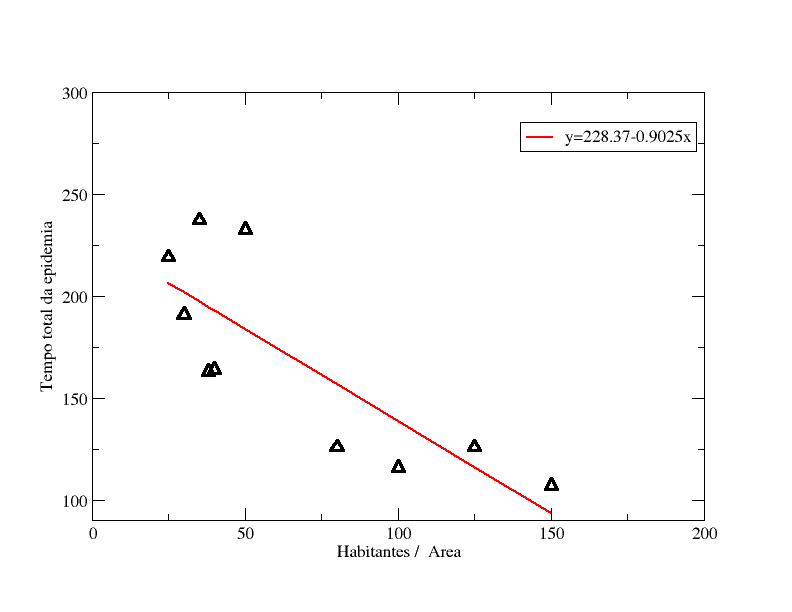
O gráfico acima relaciona a densidade populacional com o tempo total da epidemia. A curva em vermelho representa o ajuste linear dos pontos. Na minha opinião, este é o primeiro resultado contra intuitivo. A medida que a densidade populacional aumento a diminui o tempo total da epidemia.

Máximo de pessoas infectadas ao mesmo tempo

Todos os gráficos dos videos acima apresentam um pico onde o número de pessoas infectadas é máximo. No gráfico acima eu relaciono este máximo com a densidade populacional. As curvas coloridas representam os ajustes lineares.

Pessoas não infectadas

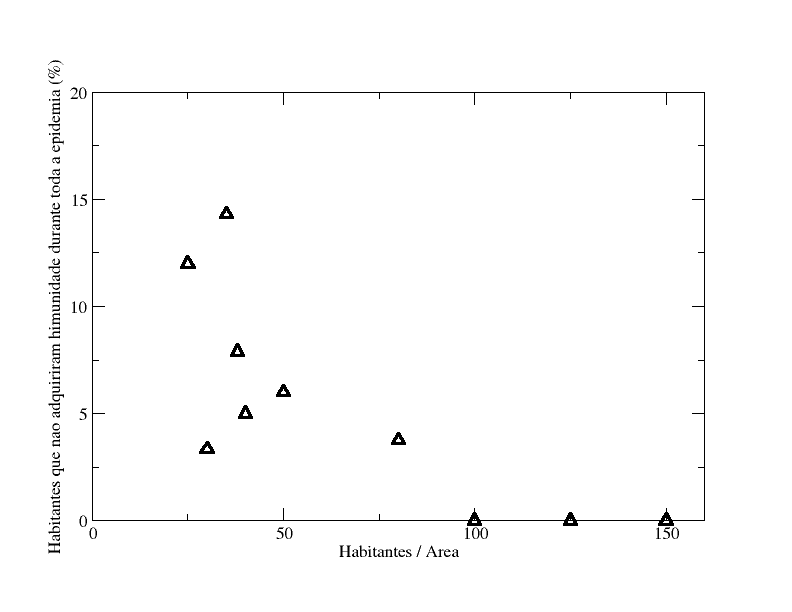
O motivo de eu exibir um gráfico para as pessoas não infectadas (veja o “glossário” acima) é simples, como elas nunca tiveram contato com a doença elas possivelmente continuam vulneráveis à doença por não terem adquirido anticorpos. Observe que quando a densidade populacional atinge um determinado patamar, não há pessoas que não tenham tido contato com a doença. Outra detalhe que pelo menos para min é bastante contra intuitivo é que mesmo as regiões pouco densas populacionalmente terem um tempo total de epidemia maior, ainda assim tem o maior número de não infectados.

Por fim, quero deixar claro que o propósito aqui é meramente didático e não deve ser considerado como uma verdade científica. Agradeço ao leitor que chegou até aqui e deixo abaixo algumas excelentes sugestões de leitura. Caso tenha alguma crítica comente abaixo.

https://www.washingtonpost.com/graphics/2020/health/coronavirus-how-epidemics-spread-and-end/

https://rothbardbrasil.com/coronavirus-o-que-e-melhor-deixar-a-epidemia-seguir-ou-achatar-a-curva/

https://www.bbc.com/portuguese/internacional-51969288

Livros:

A História da humanidade contada pelo vírus

The Anatomy of a Pandemic (English Edition)