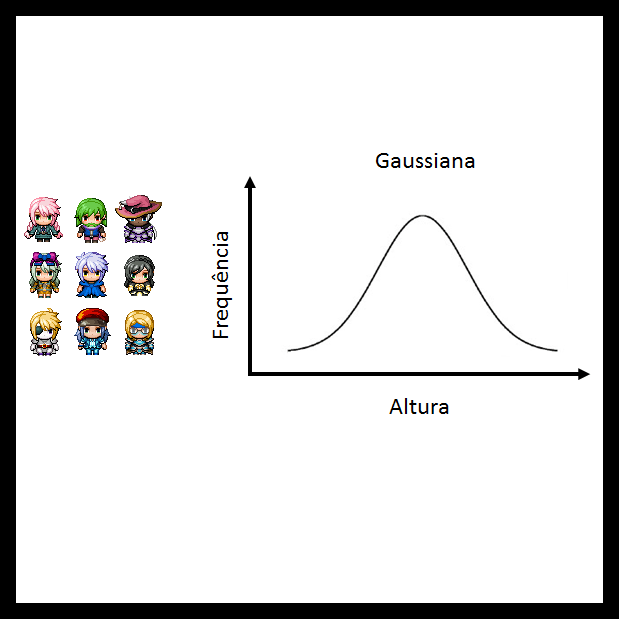
Quando somamos um conjunto de variáveis independetes com variância finita, por exemplo, a altura de um grupo aleatório de pessoas, e observarmos o comportamento da ocorrência de casos para cada altura, obtemos uma curva Gaussiana.

Paul Lévy generalizou o teorema do limite central permitindo a variância ser infinita. Desta generalização surgem as distribuições de Lévy. Essa distribuição aparece nos mais diversos tipo de sistemas natutais como no batimento cardíaco, inversão do polo magnético terrestre, no forrajeamento animal, etc.

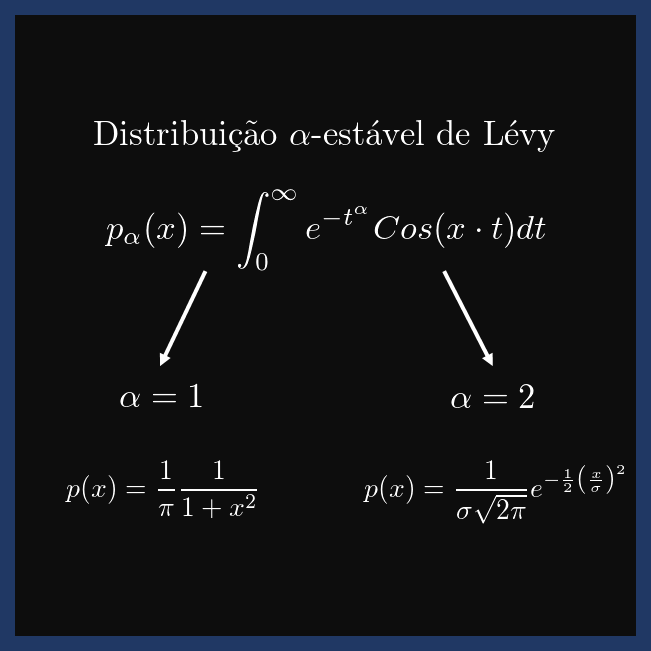
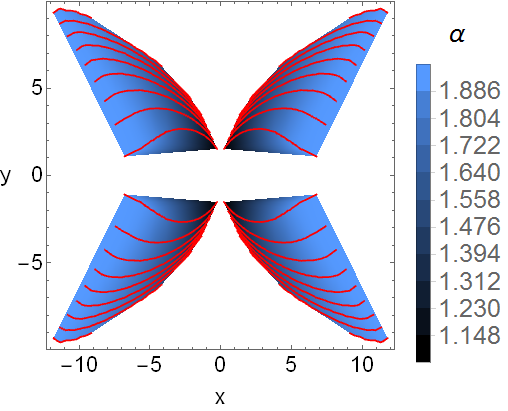
Para estudar as propriedades dessa distribuição no espaço complexo eu fiz uma animação da mesma para diversos valores de alfa. A ultima figura representa o comportamento dos zeros ds função. Nossos estudo resultou em um artigo onde entre outras coisas nós conjeturamos a não representação elementar da distribuição.